Subtitle: “Things are not as they appear, nor are they otherwise.”

For a demo (in other words, nothing matters), I wanted to take a set of rows of sample data and cluster them into a few groups approximately the same size. I figured “I’ll use a random number”. My first flaw, of course, was to decided on a solution before I fully considered the meat of the problem. But anyways…

So I fool around with RAND() in SQL and I’m not getting good results. I look online and find this Microsoft article: Selecting Rows Randomly from a Large Table. Sounds like it might have something good. They advise a syntax like this for random [see aside, at bottom]:

SELECT * FROM Table1
  WHERE (ABS(CAST(
  (BINARY_CHECKSUM(NEWID()) *
  RAND()) as int)) % 100)

Of course replacing 100 with whatever upper bound is desired.

I’ll try it out with my table:

SELECT CustomerID, 
  (ABS(CAST((BINARY_CHECKSUM(NEWID())) as int)) % 3) 
  FROM dbo.Customers

Looks good! Eyeballing indicates an approximately equal distribute of 0, 1, and 2. No other values.

Now I want to substitute a named value for each possible random value, so I put this expression into a case statement, like:

SELECT CustomerID, 
  CASE (ABS(CAST((BINARY_CHECKSUM(NEWID())) as int)) % 3) 
    WHEN 0 THEN 'Alice'
    WHEN 1 THEN 'Bob'
    WHEN 2 THEN 'Charlie'	
   END Value,
 FROM dbo.Customers

Now things get interesting. Some of the values returned are NULL! How is that possible. Furthermore, if I investigate the distribution, e.g. with:

SELECT TBL.Value, COUNT(*) FROM
(
  SELECT CustomerID, 
    CASE (ABS(CAST((BINARY_CHECKSUM(NEWID())) as int)) % 3) 
      WHEN 0 THEN 'Alice'
      WHEN 1 THEN 'Bob'
      WHEN 2 THEN 'Charlie'	
    END Value	
  FROM dbo.Customers
) TBL
GROUP BY TBL.Value

I get a very non-uniform distribution. I tried it again on a table with more rows, to get a better feel for the distribution, and found an experimental result of:

Value	Count	Approx % of Rows
Alice	696	32%
NULL	621	29%
Bob	527	24%
Charlie	311	14%

Repeated runs returned similar results. Removing the case statement and just having the inner expression resulting in an approximately uniform distribution of 0, 1, and 2.

How can this be?

I thought about it for a while and concluded that the expression must be being re-evaluated for each “when” of the case statement. This is the only thing I could come up with that would allow for the NULL possibility. But would it generate the distribution being observed? If so, that would confirm the effect.

Since we observed the generator alone was approximately normal, we’ll call it f() and say that the range of f() is {0, 1, 2} with uniform probability.

If f() is being re-evaluated at each WHEN, we end up with a probability distribution as follow:

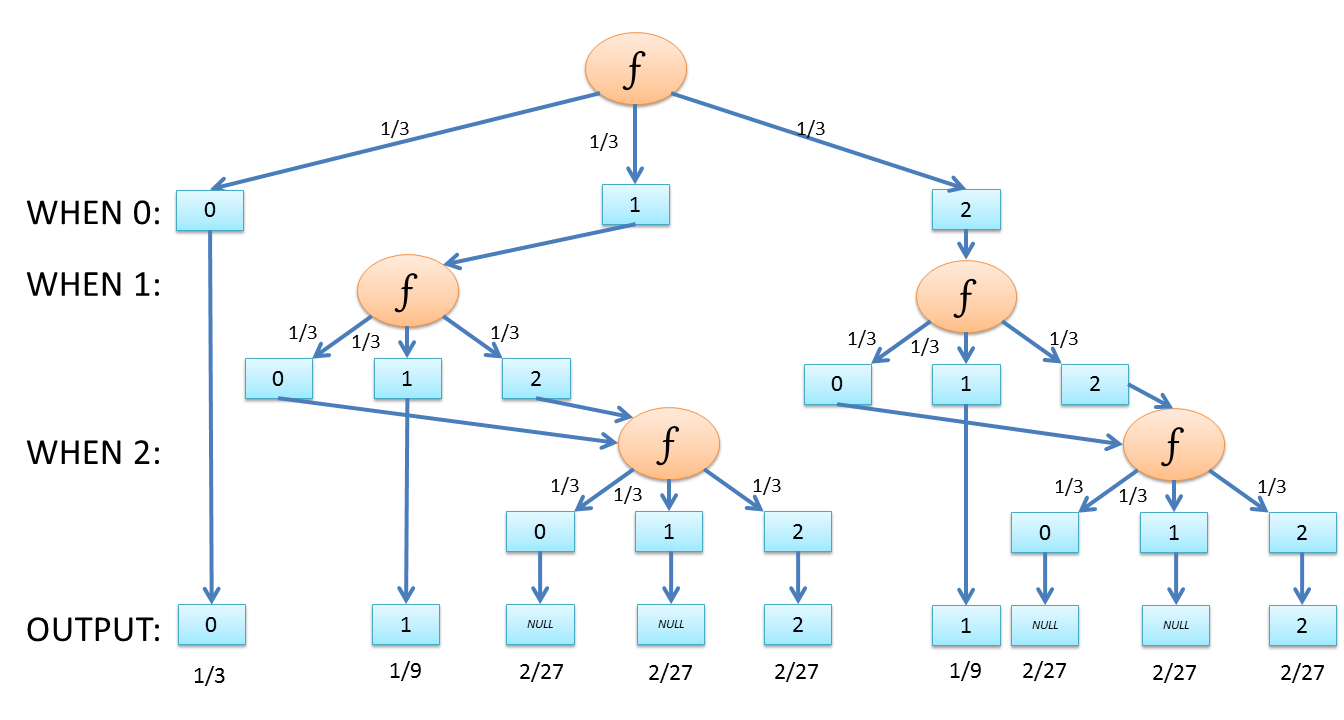
Grouping and summing the probabilities gives us:

Value	Theoretical Probability	Observed Approximate Probability
Alice (0)	1/3 = 33.3%	32%
NULL	8/27 = 29.6%	29%
Bob (1)	2/9 = 22.2%	24%
Charlie (2)	4/27 = 14.8%	14%

Theory confirms observation: f() is being re-evaluated at each WHEN.

But you already know what I’m going to tell you

Remember the whole intention of this, originally, was to arbitrarily (not necessarily randomly!) partition a set of records into several roughly equal sets. There is a much more straightforward approach if randomness is not required: simply use ROW_NUMBER().

SELECT CustomerID,
  CASE (CAST(ROW_NUMBER() OVER(ORDER BY CustomerID) AS int) % 3) 
    WHEN 0 THEN 'Alice'
    WHEN 1 THEN 'Bob'
    WHEN 2 THEN 'Charlie'	
  END Value
FROM dbo.Customers

Slight Aside

I went back and reviewed the original article and found that NEWID() is actually only advised in conjunction with other named columns. Otherwise, BINARY_CHECKSUM(*) is advised. If BINARY_CHECKSUM(*) is used, everything seems to work out fine! So, to be more specific, NEWID() (and thus, BINARY_CHECKSUM) is being re-evaluated at each row, but RAND() is not. Further, the article notes that RAND() is not needed when NEWID() or a column is specified. So, this whole problem originated in my skimming the article too quickly, and conflating two examples into one!