I was confronted by a very unusual claim by a coworker: two .NET Decimals, containing the same value, running through the same block of code, were rendering differently (one as, say, “120” and one as “120.00”). One of the big advantages of Decimal is that, unlike Float or Double, a Decimal represents an exact base-10 value whereas Float and Double are base-2, and so can only approximate many common fractional base-10 values. Therefore, I don’t normally expect problems of this kind with Decimal.
I initially assumed that the coworker was confused; some other input must be coming in, or a different section of code executing, or a different string formatting code used. However, the problem clearly reproduced. Further, it occurred even when no fractional component existed. But stripping away the extraneous, the essence of the code was fairly straightforward:
decimal v = ...; return v.ToString();
Detailed inspection revealed that in one case, the decimal value was loaded from the user input, and in another case, it was loaded from a database table. In order to test the significance of this, I made a test case which performed both side-by-side. At first, everything seems routine:
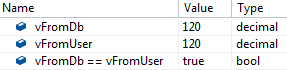
What happened next was anything but routine:
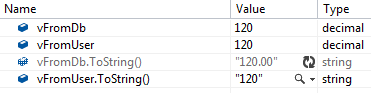
What would cause one decimal to render with 2 decimal places and another, the exact same value, to render without them? It turns out that the .NET Decimal implementation intentionally includes the concept of significant trailing zeros, which have no impact on calculations but can carry information about the value’s precision.
Although there is no direct method to expose the precision, the details of the significant trailing zeros arrangement are discussed in the Decimal.GetBits method documentation. In this case, it is clear that the same logical value can be represented with different exponents. In the case above, we can have a value of 120 with an exponent of 0, and a value of 12000 with an exponent of 2 (the exponent “indicates the power of 10 to divide the integer number”), so 12000 * 10-2 = 120.00.
This is indeed confirmed by analysis. The first three bytes contain the value, while the exponent is defined as “Bits 16 to 23” of the fourth byte.
Decimal.GetBits(vFromUser) = [120, 0, 0, 0] Decimal.GetBits(vFromDb) = [12000, 0, 0, 131072] 131072 >> 16 = 2
This confirms the vFromDb value is represented as 12000 * 10-2 while vFromUser is represented as 120 * 100. Although these values are logically equal, the default implementation of Decimal.ToString() outputs the value with all significant zeros, including trailing zeros.
Although the Decimal class does not expose properties for the precision nor the scale, it is possible to take advantage of the helper SqlDecimal class to access these values. In this context, precision means the total number of digits and scale means the number of digits to the right of the decimal place.
var sFromDb = new System.Data.SqlTypes.SqlDecimal(vFromDb); Console.WriteLine(sFromDb.Precision); Console.WriteLine(sFromDb.Scale);
For vFromDb, this outputs a precision of 5 and a scale of 2; while for vFromUser this outputs a precision of 3 and a scale of 0.
